That’s the caveman intuition: If they look alike, they probably are alike.
Who decides what “similar” means?
In the previous chapters, the author focused on how machines learn by moving through a loss landscape. We talked about bowls, gradients, and how a model slowly slides toward a point where the error is minimized.
That story was mainly about how well a machine learns.
Chapter 5 shifts the question in a subtle but important way. Instead of asking whether a model has reached the right answer, the book begins to ask how a machine decides which things belong together in the first place. Learning is about defining who counts as “close” to whom by specific learning methods like nearest neighbors and Voronoi diagrams.
The main use here, as author said, is that when we encounter a new and never-seen vector as a point in a high-dimensional space, we look at its neighbors base on the assumption that close points in space are more similar to each other. For example, if I casually write down a digit and project it into a 63-dimensional space, and the nearest labeled points are mostly “2”, then this new point is likely to be a “2” as well.
If its closest neighbors are “8”, then it is probably an “8”.
By these ways, we are no longer limited to simple visual similarity in low dimensions but can map any infomation into a vector in higher space. But this also raises a deeper question for me:
How, and under what assumptions, can we turn more complex things into points in a high-dimensional space in the first place?
Why matrices have the right to rearrange reality?
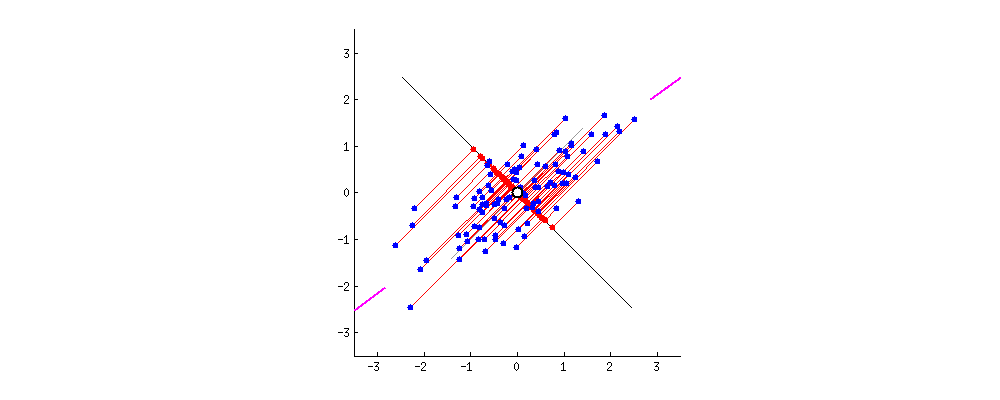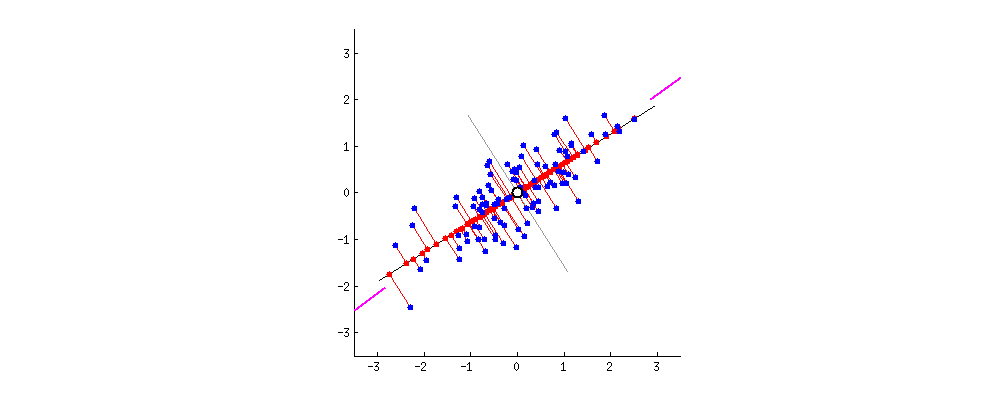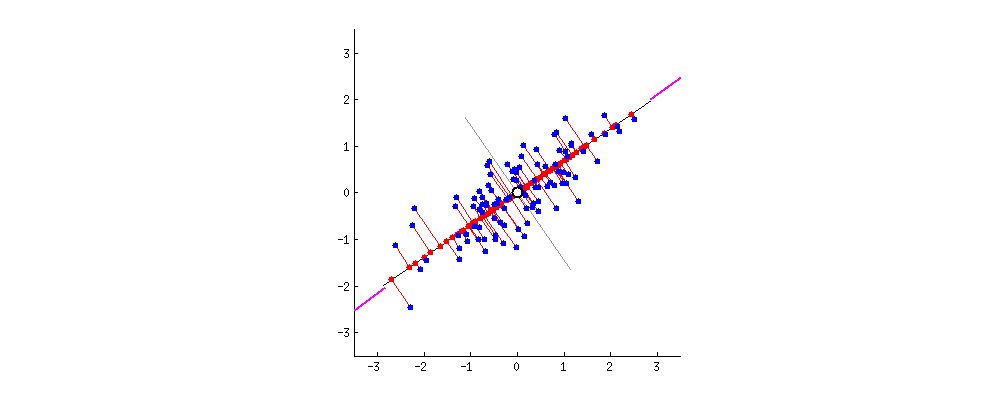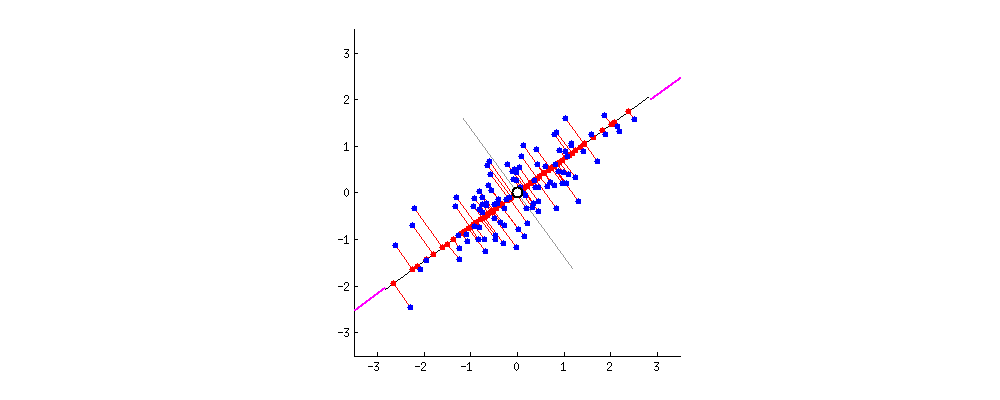
Chapter 6 answers my question in a very specific way. Instead of introducing matrices as dry tables of numbers, the author presents them as tools that can rotate, stretch, compress, and project an entire dataset. In this chapter, everything in the world becomes a long vector, with each dimension encoding a measurable feature. Since vectors can be rotated, compressed, or projected onto new axes by matrices (which can be thought of here as a stacked and extended version of vectors), we can, to some extent, rearrange reality through them.
In this chapter, the author introduces a method called principal component analysis (PCA), based on eigenvectors. PCA focuses on the dimensions along which the variation is largest and uses them as the main axes of the space. Visually, it is like turning a messy cloud of points until its structure suddenly makes sense, or begins to follow a specific direction, while the remaining variation is pushed into the background. In this way, once the data is transformed, nearest neighbors are no longer determined by raw features, but by how those features survive the transformation. In this reshaped space, who ends up close to you depends entirely on what your vector looks like after the space itself has been reconfigured.
Is similarity a fact, or a choice?
But this apparent accuracy hides a deeper assumption. Similarity only works because someone has already decided which features matter, how distance should be measured, and how the space itself should be transformed. In most cases, this process is little more than assigning numbers to enums, trying different combinations, and seeing which one works best.
Distance functions, feature selection, and matrix transformations are not neutral tools. They quietly encode judgments about what counts as important and what can be ignored. Yet they cannot explain why a particular transformation makes sense, or why a certain feature deserves a higher weight when calculating user “similarity.”
They simply play around with numbers until a relatively better result appears. And as we already concluded before, this does not mean they understand anything at all.
Closing
Chapters 5 and 6 show how powerful the mathematical ideas can be. By formalizing similarity and reshaping space, make dot product between matrices and vectors, machines can discover structure in data that would otherwise feel overwhelming. Patterns emerge, groups form, and learning becomes possible at scale.
Meanwhile, this clarity comes with a cost. Anything that does not fit neatly into the chosen features or dimensions is softened, flattened, or left behind. Differences that are hard to encode rarely survive the transformation.
What would this cause?
It simplifies the world the model gets to see. When complexity is flattened, subtle motivations, mixed identities, and shifting contexts are treated as noise rather than signal. Over time, patterns that align with the model’s assumptions are reinforced, while those that do not slowly fade from view. Recommendation systems grow more confident, but also more narrow. Difference does not disappear because it is wrong, but because it does not fit in.
Adding more dimensions seems like an obvious response. But I am not sure it really brings back what was lost. It may only give us a more spacious place to lose it in. We would see this in the next chapters.